浅谈ZKW线段树

前言

由于学业需要，本篇文章中的代码使用Python语言，可能并不能最好的体现出ZKW线段树代码的简洁性。

如果想“近距离观察”ZKW线段树的简洁和优雅，可以去文末参考博文中查看使用C++写的代码。

一、引入

1.为什么要创造线段树

如果存在一个数组，我们需要经常的修改其中的数据，同时又需要经常的读取其中某个片段的和。

假设arr为这个数组：

arr 1 3 5 7 9 11

  • 此时我们对他进行update操作，比如修改 7 这个元素，我们可以直接访问这个元素的下标，那么此时update方法的时间复杂度为O(1)。

  • 如果我们想对他进行query操作，比如求第2个元素到第5个元素的和，我们需要遍历2、3、4、5这几个元素，如果想求第n个到第2n个元素的和，那么此时query方法的时间复杂度为O(n)。

当然，我们可以再创建一个sum_arr数组，使用差分的方法，每个位置都存放arr数组中对应位置及之前所有元素的和：

sum_arr 1 4 9 16 25 36
  • 此时我们对他进行query操作，还是求第2个元素到第5个元素的和，只需要访问sum_arr中第5个元素的下标和第2个元素的下标，将他们所存放的值相减，即可得到我们想要的和。我们成功的将query方法的时间复杂度降低到了O(1)。
  • 但如果我们对他进行update操作，还是修改 7 这个元素。我们会发现，由于此时我们需要同时维护两个数组，所以当我们改变arr数组中的元素值后，需要同时对sum_arr中对应位置及其之后所有位置储存的值进行修改。此时，update方法的时间复杂度又降为了O(n)。

综上所述，如果我们需要进行的query和update操作一样多的前提下，无论我们使用以上两种方法中的哪个，我们所进行的操作总体速度都不会特别的快。

而这时使用线段树，就可以将query和update操作的时间复杂度通通降为O(log n)。

2.什么是线段树

线段树是一种特殊的平衡二叉搜索树。

什么叫做二叉搜索树？首先满足二叉树，每个结点度小于等于二，即每个结点最多有两颗子树。何为搜索？我们要知道，线段树的每个结点都存储了一个区间，也可以理解成一个线段，而搜索，就是在这些线段上进行搜索操作得到你想要的答案。

线段树的适用范围很广，可以在线维护修改以及查询区间上的最值，求和。

把上面说过的数组变成线段树即为这个样子：

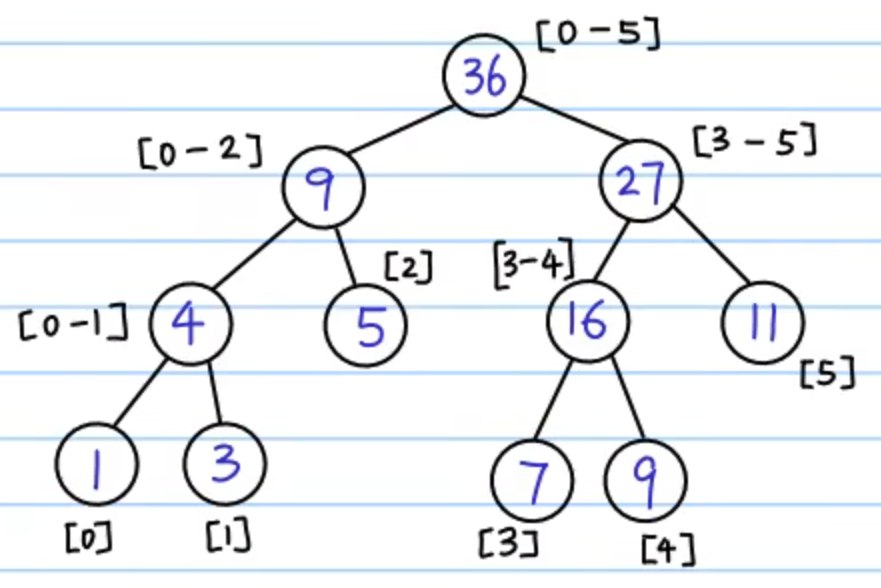
query 操作：
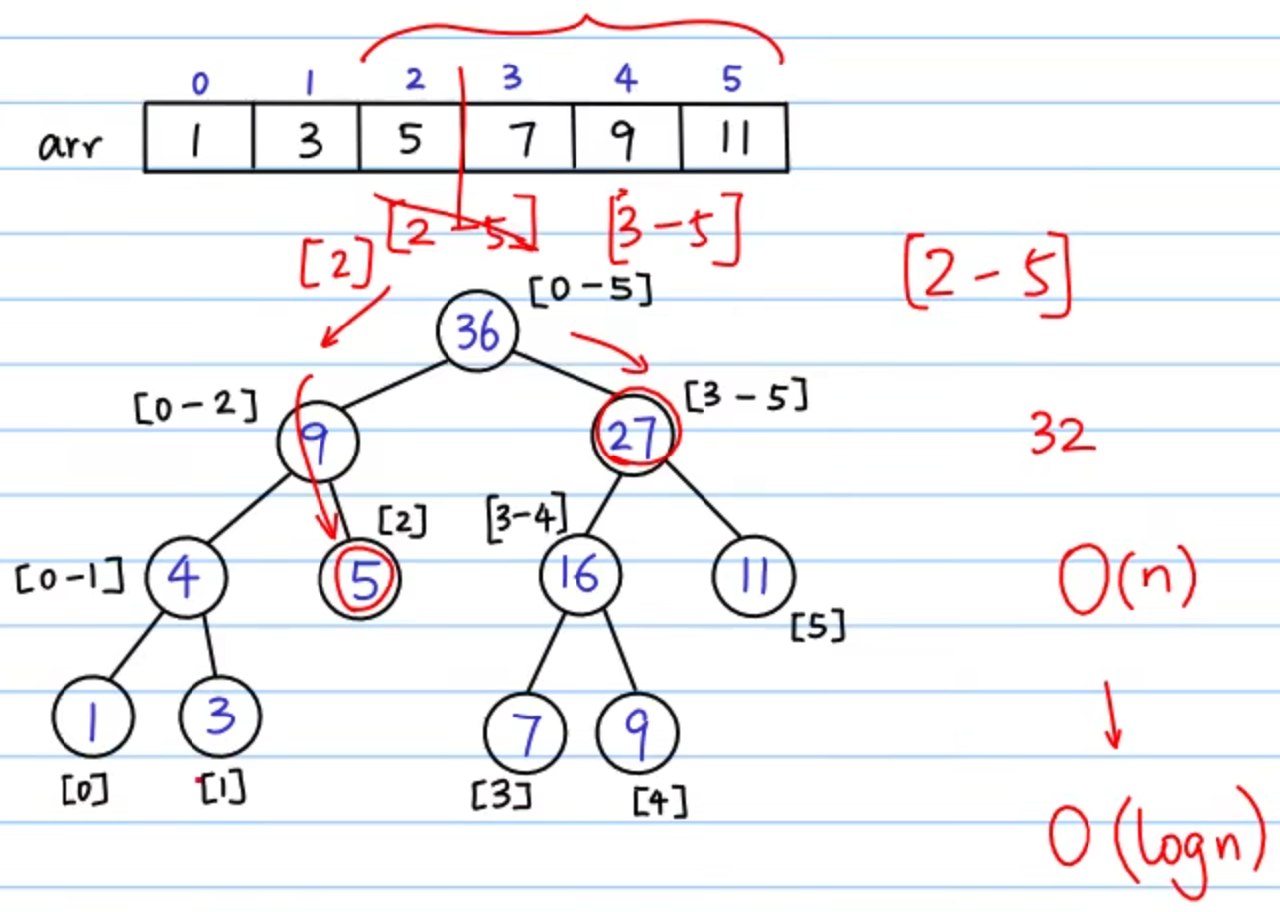
update 操作：
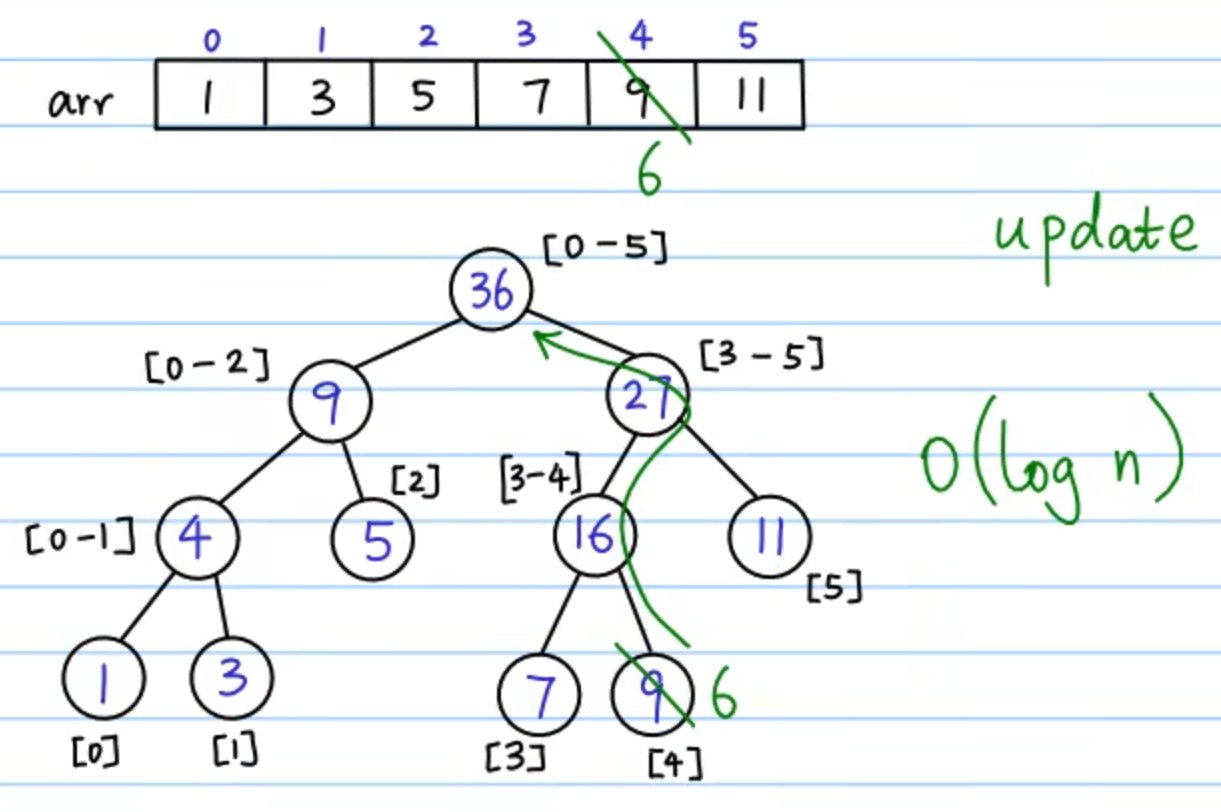
存放和索引
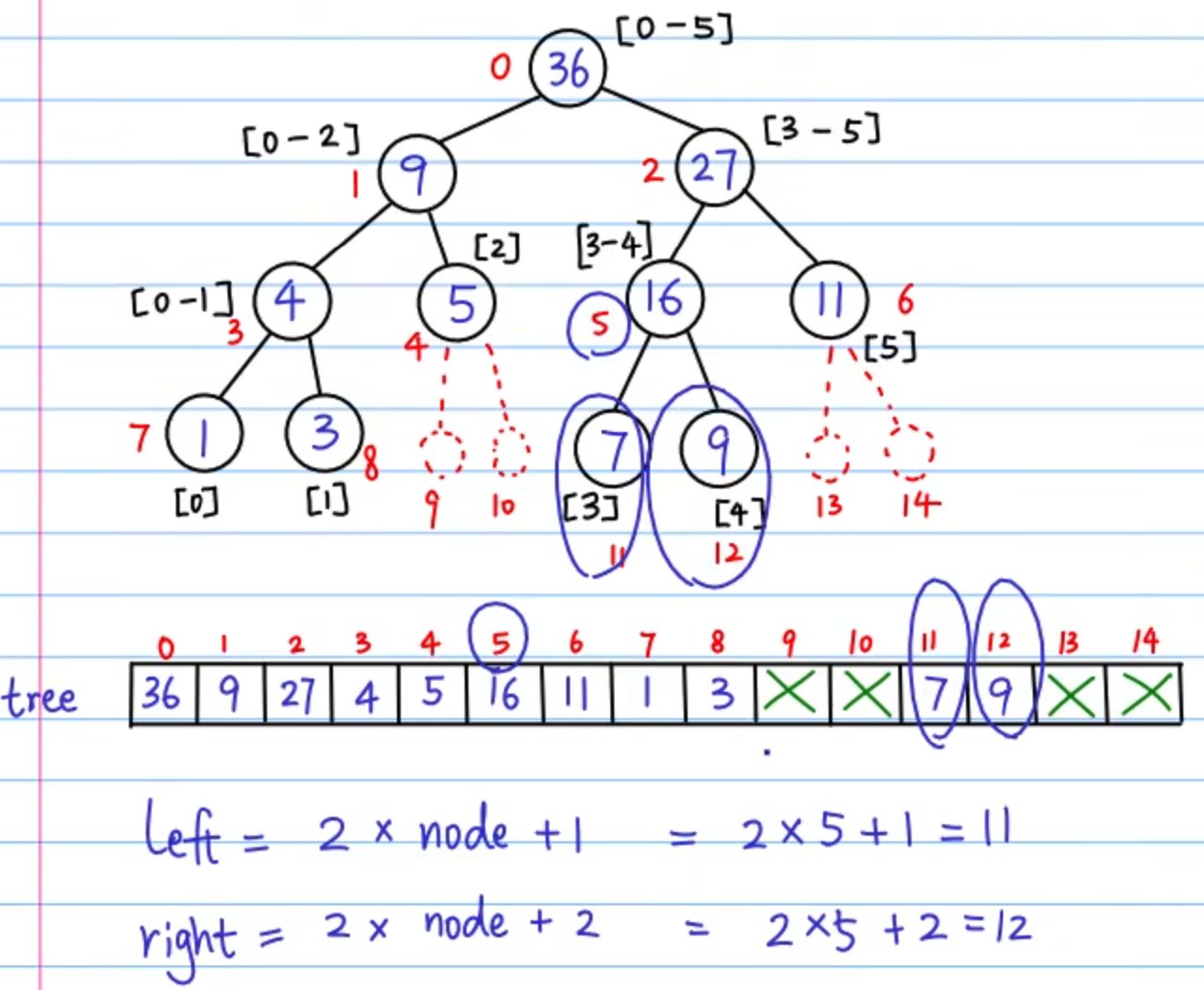
普通线段树的问题

上述已经说明线段树的优点以及线段树的逻辑结构和物理结构，但是实际上的线段树并没有想象中的那么美好，他既不简洁，也不高效，又不优雅。

  • 不简洁：线段树的构建、单点修改、区间修改、单点查询、区间查询的代码实现都比较冗长。
  • 不高效：他的构建以及各种方法都通过递归实现，所以他的常数极大，如果在处理大量数据时，容易造成栈溢出。
  • 不优雅：线段树需要同时维护两个数组，即原数组和tree数组。

二、ZKW线段树

1.介绍

实际上线段树是不需要递归的，有一些方式可以实现非递归线段树以减少递归开销。

ZKW 线段树就是一种不错的非递归解决方案。

它是由一位清华大佬张昆玮发明的一种非递归线段树，采用了二进制位运算的方式计算节点，所以具有相当优秀的常数，在一般 RMQ 问题中使用时间常数约为普通线段树的1/2 ~ 1/4，树状数组和 ST 表的4/5 ~ 5/2倍，算是相当优秀了。

同时，ZKW线段树的整体代码给人了一种树状数组的简洁感
所以说，ZKW线段树是一个真正意义上简洁、高效、优雅的数据结构。

2.建树

这是一个长度为4的线段对应的二叉树，树上的每个节点对应的权值就是每个节点编号的二进制表示。可见第三层的节点右移一位之后，就变成了他们的父节点。同理，第二层中的结点也可以通过相同的方式变成根节点。

看起来和普通的线段树一样，都是堆存储，不过，这棵树其实是可以使用普通的循环方式存下来的。

过程：

我们先设置一个变量bit表示这棵线段树非叶子节点的总数，可以通过循环移位的方式拿到：

1
2
3
4
n = len(arr)
bit = 1
while bit <= n + 1:
    bit <<= 1

然后给所有叶子节点赋值：

1
2
3
tree = [0 for _ in range(2 * bit)]
for i in range(1, n + 1):
    tree[bit + i] = arr[i-1]

接下来，向上传递，只需要倒序遍历非叶子节点（保证层数从下向上传递），然后加和即可：

1
2
for i in range(bit - 1, 0, -1):
    tree[i] = tree[i << 1] + tree[(i << 1) | 1]

完整代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def buuld_tree(arr):
    # 获取bit大小
    n = len(arr)
    bit = 1
    while bit <= n + 1:
        bit <<= 1
    # 初始化tree数组及叶子节点
    tree = [0 for _ in range(2 * bit)]
    for i in range(1, n + 1):
        tree[bit + i] = arr[i-1]
    # 更新非叶子节点
    for i in range(bit - 1, 0, -1):
        tree[i] = tree[i << 1] + tree[(i << 1) | 1]
    return tree, bit
解析：

ZKW线段树的tree数组中，前半部分存的是所有非叶子节点，后半部分存的是所有叶子节点（即原数组的值），所以我们只需要维护这一个数组就可以，通过是否+bit的方式来决定访问非叶子节点还是叶子节点。

同时，访问时也只需要根据当前地址进行位移就可以访问父、子节点。

i >> 1右移访问父节点，i << 1左移访问左孩子节点，i << | 1左移加1访问右孩子节点。（可参考上面图片理解）

3.单点修改

单点修改非常简单，他的思想就是先把叶节点修改，然后依次维护父节点（把所有和它有关的的修改掉）。

先找到它对应在树上的叶子节点，然后一直找父亲传递就好了：

1
2
3
4
5
6
7
8
9
def update_point(tree, bit, pos, new_value):
    # 找到并修改叶子节点
    pos += bit
    tree[pos] = new_value
    # 右移找到父节点
    pos >>= 1
    while pos > 0:
        tree[pos] = tree[pos << 1] + tree[(pos << 1) | 1]
        pos >>= 1

4.单点查询

没什么好说的，直接访问对应pos + bit：

1
2
3
def query_point(tree, bit, pos):
    index = bit + pos
    return tree[index]

5.区间查询

区间查询可能有些难理解，与普通线段树的top->down不同，ZKW线段树使用的是bottom->up的思路。

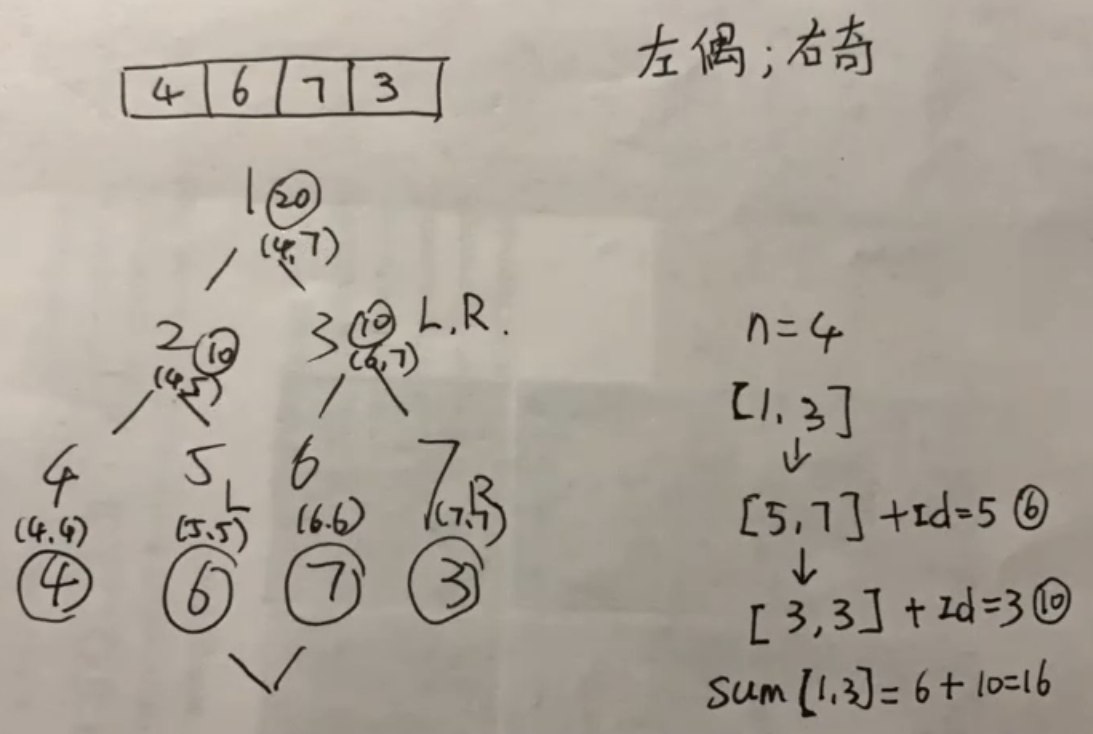
比如我们想要查询 6 到 3 ，这时L在index=1+bit=5的位置，R在index=3+bit=7的位置。

区间查询函数中有一个规则：

  • 当L所在的节点为右孩子的时候，以当前L的值更新返回值，并把 L+1
  • 当R所在的节点为左孩子的时候，以当前R的值更新返回值，并把 R-1

这是因为L为右孩子时，说明他左边的所有元素都需要丢掉，包括他的父节点；而R为左孩子时，说明他右边的所有元素都需要丢掉，包括他的父节点。

当进行完这两个判断后，将L和R全都右移，即移动到他们的父节点。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def query_range(tree, bit, L, R):
    # 将L、R移动到对应叶子节点
    L += bit
    R += bit
    # 初始化返回值
    num = 0

    while L <= R:
        if L & 1:	# 如果L是右孩子
            num += tree[L]
            L += 1

        if not R & 1:	# 如果R是左孩子
            num += tree[R]
            R -= 1
        # 将L、R移动到对应父节点
        L >>= 1
        R >>= 1

    return num

6.区间修改

这里是整个ZKW线段树中最复杂的部分，由于时间原因，先不写这个功能了，程序中也没有用到。

参考

本文参考了：